# Codice per fare i fit
# Utile se vogliamo visualizare in una finestra i picchi per stimare i punti
# %matplotlib qt
# ---------0 ----------1 -----------2 ----------3 ----------4 ----------5 -------------6 -------
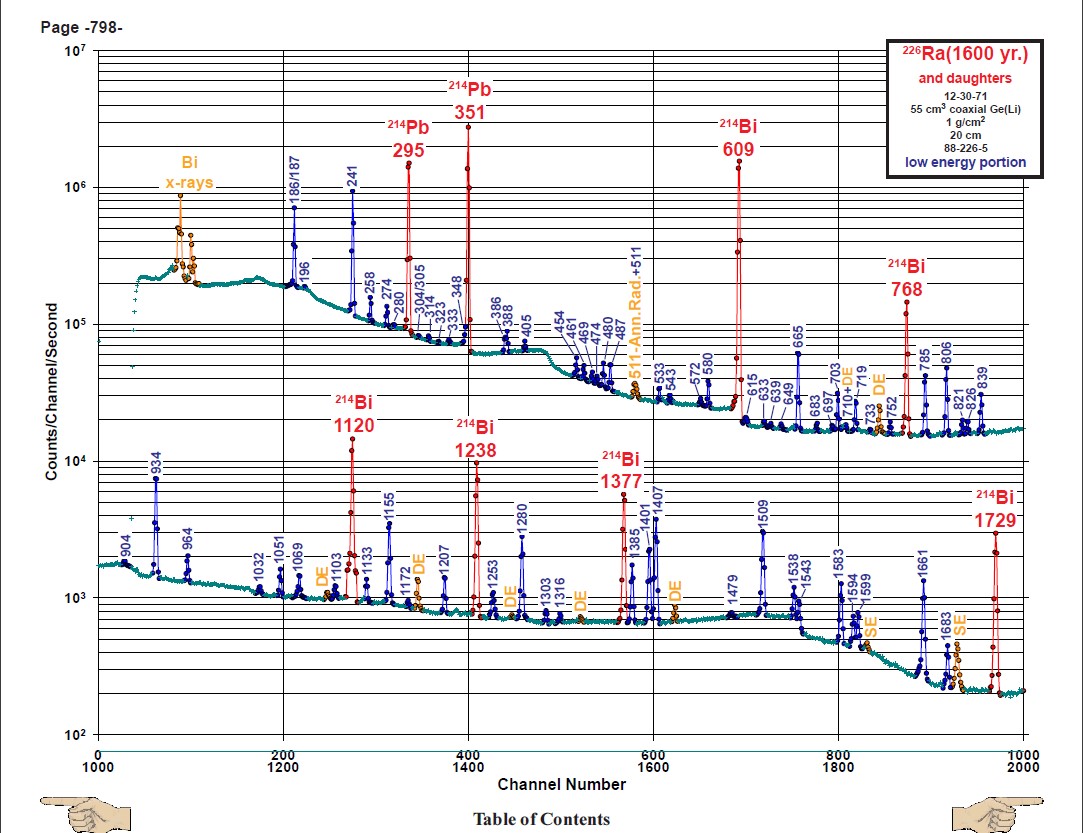
energieVere = np.array((77, 185, 241, 295, 351, 609, 1120))
# Alcuni parametri per il fit
myRange = ((260, 358), (492, 590), (590, 704), (704, 825), (806, 971), (1296, 1556), (2305, 2600))
startPars = ((3.14020187e+05, 2.98589322e+02, 1.43257226e+01),
(9.41411082e+04, 5.34214983e+02, 2.02581202e+01),
(1.04459955e+05, 6.51821651e+02, 2.23514168e+01),
(2.30961972e+05, 7.65474019e+02, 2.49634128e+01),
(3.65195534e+05, 8.86502718e+02, 2.82249031e+01),
(.215e5, 1422, 41.2),
(9.82593192e+04, 2.47588684e+03, 1.06711679e+02),)
# Inizializzo due liste in cui vado a memorizzare i parametri estratti dal fit
lstPopt = []
lstPcov = []
# Definisco una funzione comoda per poter raggruppare le stesse operazioni da effettuare varie volte
def myFun(axx, idx):
# Seleziono il range in cui fare il fit
tmpCond = (binc > myRange[idx][0]) & (binc < myRange[idx][1])
# Definisco gli starting points
tmpp0 = (*startPars[idx], 7.81582354e+03, 2.32745796e-03)
# Effettuo il fit
popt, pcov = curve_fit(funcToFit, binc[tmpCond], h[tmpCond], p0 = tmpp0,
sigma = np.sqrt(h[tmpCond]), absolute_sigma = True)
# Memorizzo i parametri
lstPopt.append(popt)
lstPcov.append(pcov)
# Plotto le curve fittate
#axx.plot(binc[tmpCond], funcToFit(binc[tmpCond], *tmpp0), ls = ":", c = "r")
axx.plot(binc[tmpCond], funcToFit(binc[tmpCond], *popt), ls = "--", lw = 2,
label = f"Picco {idx+1} - $\mu=$ {popt[1]}")
# Rifaccio il plot dell'istogramma definito nella cella precedente
fig, ax = plt.subplots()
fig.set_size_inches(12,5)
ax.plot(binc, h, ds = "steps-mid", c = "k", label = "Dati $^{226}$Ra", lw= .5 )
# Vao a richiamare la funzione per ciascun picco
for i in range(7): myFun(ax, i)
# Alcune impostazioni grafiche del plot
ax.set_title("Spettro", fontsize = 16)
ax.set_xlabel("Energia [ADC]", fontsize = 14)
ax.set_ylabel("Entries", fontsize = 14)
ax.grid(True)
ax.set_yscale("log")
ax.legend(fontsize = 10, framealpha = .3)
plt.show()