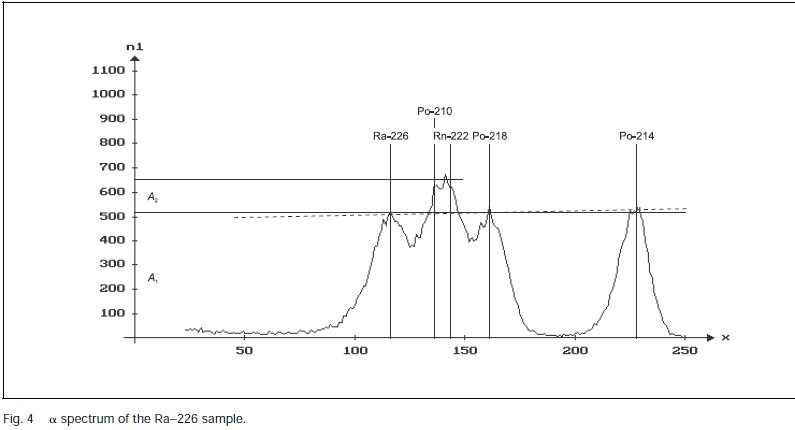
%matplotlib inline
def gaus3Line(x,a1,mu1,sigma1,a2,mu2,sigma2,a3,mu3,sigma3,m,q):
return a1/(sigma1*np.sqrt(2*np.pi)) * np.exp( -(x-mu1)**2 / (2*sigma1**2)) + a2/(sigma2*np.sqrt(2*np.pi)) * np.exp( -(x-mu2)**2 / (2*sigma2**2)) + a3/(sigma3*np.sqrt(2*np.pi)) * np.exp( -(x-mu3)**2 / (2*sigma3**2)) + m*x+q
def gaus(x,a,mu,sigma, m, q):
return a/(sigma*np.sqrt(2*np.pi)) * np.exp( -(x-mu)**2 / (2*sigma**2)) +m*x+q
# Inizio plot
fig, ax = plt.subplots()
fig.set_size_inches(12,5)
ax.plot(binc, h, ds = "steps-mid", c = "darkgreen", lw = 2, label = "Spettro")
ax.fill_between(binc, h, step = "mid", color = "lime", alpha = 1)
# FIT SX
cond = (binc >930) & (binc < 1871)
xData = binc[cond]
yData = h[cond]
popt, pcov = curve_fit(gaus3Line, xData, yData, sigma = np.sqrt(yData), absolute_sigma = True,
p0 = (
3789330, 1277, 50,
20966339, 1496, 50,
3789330, 1706, 50,
-3,5000), maxfev = 100000)
xDenso = np.linspace(xData.min(), xData.max(), num = 500)
ax.plot(xDenso, gaus3Line(xDenso, *popt), "--b", lw=3, label = "Curva fittata")
# FIT DX
cond = (binc >2106) & (binc < 2463)
xData = binc[cond]
yData = h[cond]
poptdx, pcovdx = curve_fit(gaus, xData, yData, sigma = np.sqrt(yData), absolute_sigma = True,
p0 = (5049244, 2315, 20, -3,500), maxfev = 100000)
xDenso = np.linspace(xData.min(), xData.max(), num = 500)
ax.plot(xDenso, gaus(xDenso, *poptdx), "--b", lw=3)
# Fine plot
ax.grid()
ax.set_xlabel("Energia [ADC]", fontsize = 14)
ax.set_ylabel("Entries", fontsize = 14)
ax.set_title("Spettro", fontsize = 16)
ax.legend()
#ax.set_yscale("log")
plt.show()